足球的表面積是多少（快樂說數(shù)：球的體積和表面積）

　　數(shù)學(xué)看上去枯燥無味，其實不然，掌握正確的學(xué)習(xí)方法，我們就能做到快樂學(xué)數(shù)學(xué)。學(xué)好數(shù)學(xué)大致能分為三個步驟：第一，梳理好知識點；第二，學(xué)好各種題型；第三：針對所學(xué)知識訓(xùn)練鞏固。

　　現(xiàn)在我們來看今天要學(xué)的內(nèi)容，先看下邊球的體積和表面積的思維導(dǎo)圖：

　　

　　

　　接著我們針對球的體積和表面積展開來講，首先是知識梳理：

　　知識點一　球的體積公式與表面積公式

　　1.球的體積公式V＝πR3(其中R為球的半徑).

　　2.球的表面積公式S＝4πR2.

　　思考　球有底面嗎？球面能展開成平面圖形嗎？

　　答　球沒有底面，球的表面不能展開成平面.

　　知識點二　球體的截面的特點

　　1.球既是中心對稱的幾何體，又是軸對稱的幾何體，它的任何截面均為圓，它的三視圖也都是圓.

　　2.利用球半徑、截面圓半徑、球心到截面的距離構(gòu)建直角三角形是把空間問題轉(zhuǎn)化為平面問題的主要途徑.

　　接著是題型分類：

　　題型一　球的表面積和體積

　　例1　(1)已知球的表面積為64π，求它的體積；

　　(2)已知球的體積為π，求它的表面積.

　　解　(1)設(shè)球的半徑為R，則4πR2＝64π，解得R＝4，

　　所以球的體積V＝πR3＝π·43＝π.

　　(2)設(shè)球的半徑為R，則πR3＝π，解得R＝5，

　　所以球的表面積S＝4πR2＝4π×52＝100π.

　　反思與感悟　1.已知球的半徑，可直接利用公式求它的表面積和體積.

　　2.已知球的表面積和體積，可以利用公式求它的半徑.

　　題型二　球的截面問題

　　

　　反思與感悟　有關(guān)球的截面問題，常畫出過球心的截面圓，將問題轉(zhuǎn)化為平面中圓的有關(guān)問題解決.

　　題型三　球的組合體與三視圖

　　

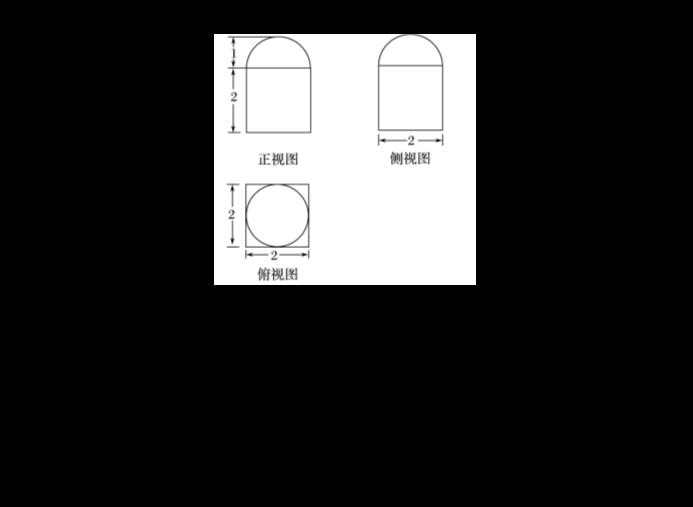
　　反思與感悟　1.由三視圖求球與其他幾何體的簡單組合體的表面積和體積，關(guān)鍵要弄清組合體的結(jié)構(gòu)特征和三視圖中數(shù)據(jù)的含義.

　　2.求解表面積和體積時要避免重疊和交叉.

　　最后是試題訓(xùn)練，并附上答案及解析：

　　

　　

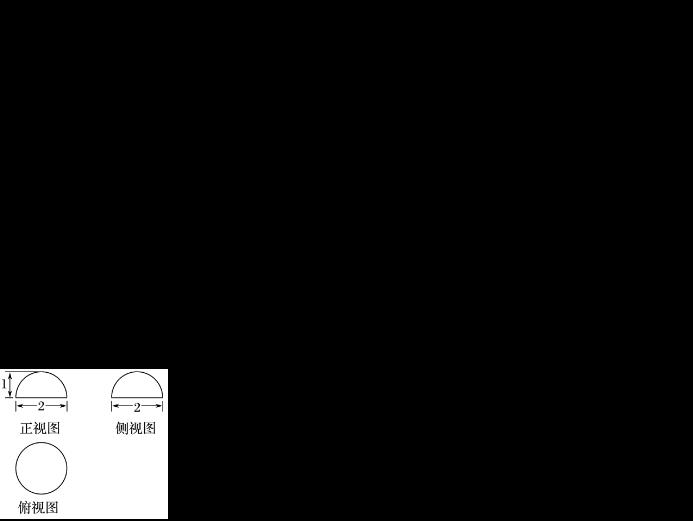
　　希望大家都有所收獲，現(xiàn)在是必修二系列的知識，大家可以往前翻看。大家關(guān)注我，之后還有精彩內(nèi)容哦！

結(jié)尾，以上就是足球的表面積是多少（快樂說數(shù)：球的體積和表面積）的文章整合